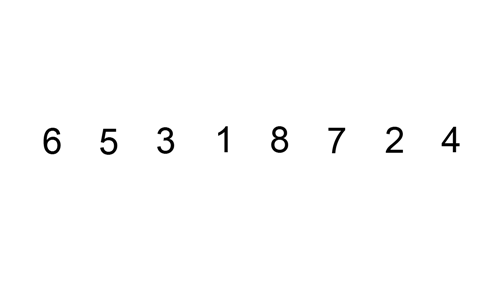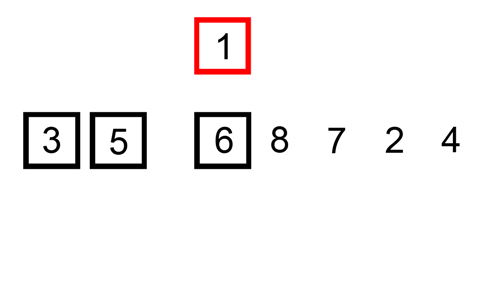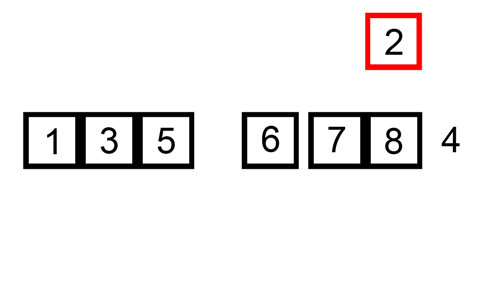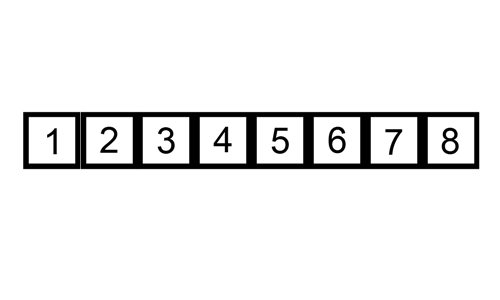Sıralama Algoritmaları – I

Merhaba bu yazımda sıralama algoritmalarını inceleyeceğim. Sıralama algoritmaları çoğumuza üniversite ders sıralarında kalmış görünse de aslında gündelik hayatımızda kullandığımız hemen hemen her teknik aracın işleyişinde rol alıyor. Bundan otuz kırk yıl önce bilgisayar teknolojisinin sunabileceği işlemci, bellek ve sabit disk gibi kaynaklar oldukça sınırlıydı, bu yüzden yapılacak işler için etkili yöntemler kullanmak gerekiyordu. Günümüzde bu kaynaklar kolay erişilebilir hale geldi ama yine de etkili yöntemler kullanmamız gerekiyor. Çünkü hala çok daha etkili kullanmak zorunda olduğumuz bir kaynak olan zaman katı bir kısıt olarak karşımızda duruyor.

Çok basit şekilde yaklaşalım, verimliliğe ve karmaşıklığa dikkat etmediğimiz çok büyük sayıda girdiye sahip kötü bir program geliştirdiğimizi düşünelim (lütfen bu sadece kötü bir varsayım olarak kalsın). Bu programı şu an dünya üzerinde bulunan en gelişmiş bilgisayarda çalıştırma fırsatını bulabiliriz ama bu programın sonuç vermesi için gereken birkaç yılı bulamayız. O yüzden tercihimizi daha az zaman karmaşıklığı içeren algoritmalardan yana kullanmak mantıklı bir yaklaşım olacaktır.

Sıralama algoritmalarını inceleme için takip edeceğim temel kaynak R. Sedgewick ve K. Wayne’nin Algorithms* kitabı olacaktır. Ben de kitaptaki yaklaşımı sürdüreceğim ve sıralama algoritmalarını basit ve gelişmiş olarak iki ana sınıfa ayıracağım. Basit sıralama algoritmaları olarak Seçmeli Sıralama (Selection sort) ve Eklemeli Sıralama’yı (Insertion sort) inceleyeceğim. Gelişmiş sıralama algoritmaları olarak Birleştirmeli Sıralama (Mergesort) ve Hızlı Sıralama’yı (Quicksort) inceleyeceğim.

Basit Sıralama Algoritmaları

1. Seçmeli Sıralama

Seçmeli sıralama, adını dizi içerisindeki en küçük elemanı seçtiği için almıştır. Bu algoritma şu şekilde çalışır: Dizi içerisindeki en küçük elemanı bulup ilk elemanla değiştirir, daha sonra en küçük diğer elemanı bulup ikinci elemanla değiştirir, dizi tamamen sıralanana kadar her defasında en küçük elemanı bulup dizide yerine yerleştirir. Algoritmanın çalışma şeması aşağıdaki gibidir.

Algoritmanın Java dilindeki örnek kodunu aşağıda görebilirsiniz.

public void selectionSort(Array a) {
    int N = a.length;
    for(int i=0; i< N; i++) {
        int min = i;
        for(int j=i+1; j<N; j++) {
            if(a[j] < a[min]) {
                min = j;
            }
        }
        exchange(a[i], a[min]);
    }
}

Seçmeli sıralama algoritmasının karmaşıklığını hesaplamak için, yapılan karşılaştırma ve yer değiştirmeler hesaplanır. Algoritma N elemanlı bir dizide en küçük eleman için N-1 tane karşılaştırma yapar, ikinci en küçük eleman için N-2 tane karşılaştırma yapar, diğer elemanlar için karşılaştırma sayısı N-3, N-4,…, 2, 1, 0 şeklinde devam eder, en son eleman için 0 karşılaştırma yapar. Tüm karşılaştırmaları toplarsak,
(N-1) + (N-2) + (N-3) + (N-4) + … + 2 + 1 + 0 = N(N-1) /2
elde ederiz. Her bir eleman için bir yer değiştirme yapılır, tüm dizi için toplam N tane yer değiştirme işlemi yapilir. Hesaplamalar sonucunda elde edilen
N(N-1)/2 + N ~ N²
değerlerinin asimptotik üst sınırı O(N²) değerini verir.

*Seçmeli sıralama algoritması O(N²) karmaşıklığıyla çalışır.

2. Eklemeli Sıralama

Eklemeli sıralama, adını seçilen elemanın daha sonra yerine yerleştirilmesinden alır. Seçilen ilk eleman ayrı bir yere kopyalanır, seçilen eleman kendisinden küçük indeksli elemanlarla karşılaştırılır, kendisinden büyük olan elemanlar birer sıra sağa kaydırılır ve seçilen eleman yerine yerleştirilir. Dizinin son elemanı yerleştirilince dizi sıralanmış olur. Algoritmanın çalışma şeması aşağıdaki gibidir.

Algoritmanın Java dilindeki örnek kodunu aşağıda görebilirsiniz.

public void insertionSort(Array a) {
    int N = a.length;
    for(int i=1; i<N; i++) {
        for(int j=i; j > 0 && a[j] < a[j-1]; j--) {
            exchange(a[j],a[j-1]);
        }
    }
}

Eklemeli sıralama algoritmasının karmaşıklığını hesaplamak için, yapılan karşılaştırma ve yer değiştirmeler hesaplanır. Algoritma N elemanlı bir dizide ikinci eleman için en fazla 1 karşılaştırma ve 1 yer değiştirme yapar, üçüncü eleman için 2 karşılaştırma ve 2 yer değiştirme, dördüncü eleman için 3 karşılaştırma ve 3 yer değiştirme yapar. Bu şekilde son eleman için en fazla N-1 karşılaştırma ve N-1 yer değiştirme yapar. Dizinin tüm elemanları için yapılacak en fazla karşılaştırma ve yer değiştirme işlemlerini topladığımız zaman,
2(1 + 2 + 3+ 4+ … + N-2 + N-1) = 2(N(N-1)/2) = N(N-1)
buluruz.
Hesaplamalar sonucunda elde edilen
N(N-1) ~ N²
değerinin asimptotik üst sınırı O(N²) değerini verir.

*Eklemeli sıralama algoritması en kötü durumda (örneğin dizi tersten sıralıysa) O(N²) karmaşıklığıyla çalışır.

*Dizi sıralıysa sadece N-1 kez karşılaştırma yapar ve O(N) karmaşıklığıyla çalışır, en iyi performansı O(N)‘dir.

*Eklemeli sıralama algoritmasının ortalama performansı ise yine O(N²) değeridir.

Değerlendirme

Seçmeli ve Eklemeli sıralama algoritmalarını kıyaslarsak, seçmeli sıralama algoritması listenin en küçük elemanının nerede olduğunu bilmediği ve her bir eleman için tüm elemanlarla karşılaştırma yaptığı için liste içindeki elemanların rasgele sıralanmış ya da eşit elemanlardan oluşmasını dikkate almaz, bu sebeple seçmeli sıralama algoritması her durumda O(N²) karmaşıklığıyla çalışır.
Fakat Eklemeli sıralama algoritması, dizinin sıralı olmasını dikkate alır ve eğer dizinin çoğu sıralıysa O(n) karmaşıklığıyla çalışır. Eklemeli sıralama algoritması, eleman sayısı az olan ya da bir kısmı sıralı küçük boyutlu diziler için oldukça uygun bir sıralama algoritması seçimidir.

Kaynaklar
*1. Robert Sedgewick, Kevin Wayne, Algorithms 4th Edition, Addison-Wesley 2011 (chapter 2 p. 248-250).
2. http://www.sorting-algorithms.com/, en son 21.03.2015 tarihinde erişildi.
3. https://en.wikipedia.org/wiki/Selection_sort, en son 21.03.2015 tarihinde erişildi.
4. https://en.wikipedia.org/wiki/Insertion_sort, en son 21.03.2015 tarihinde erişildi.